1. Introduction
A major problem in making effective use of computers is dealing with complexity. As we design programs of increasing functionality, we find ourselves overwhelmed by their ever greater complexity. It might seem that the complexity of computational systems must be limited by our ability to understand and design them, but this is not so. In the world outside computation are working systems that developed without design-indeed, systems of a complexity far beyond present design capabilities [1].
A patterned system which develops without deliberate design is termed a spontaneous order [2]. Crystals provide a simple example: nowhere in the nature of an element’s individual atomic forces is its crystal structure specified, much less designed, yet that structure emerges as a result of those forces. Similar examples include patterns observed in Conway’s game of Life [3] and the spiral arms of galaxies. A particularly powerful spontaneous ordering principle is evolution. Among the spontaneous orders in the world, the most intricate and impressive are those-such as human bodies and languages-that have emerged through evolutionary processes.
The goal of this work is to understand how to build systems that will develop increasingly effective (even intelligent) computation through spontaneous ordering processes. In pursuit of this goal, this paper examines several evolutionary systems to determine which properties will serve best when generalized to the computational domain.
Biology provides the most familiar examples of evolutionary processes. A simple generalization from these examples might suggest that evolution is necessarily slow, and that it must proceed by random mutations. But human culture-including technology and scientific know- ledge-is also a result of evolutionary processes [2,4]. This shows that evolution can proceed quickly, and that “mutations” in an evolving system can result from thought and design. The essence of evolution is trial and the weeding out of error, but the trials need not be random.
Evolution often proceeds in what, in the biological case, is called an ecosystem. Here, the concept of an ecosystem is generalized to cover any set of evolving, interacting entities operating within a framework of rules.
Ecosystems vary in their ability to solve externally defined problems. One can imagine putting a person or an ecosystem in a box and then presenting problems and contingent rewards through a window in the box. A box full of algae and fish will “solve” a certain narrow set of problems (such as converting light into chemical energy), and will typically pay little attention to the reward. A box containing an intelligent person will solve a different, broader range of problems. A box containing, say, an industrial civilization (with access to algae, fish, and Bell Labs) will solve a vastly greater range of problems. This ability to solve externally posed problems can be taken as a measure of an ecosystem’s “intelligence” (see Section 6.2 of [I]).
Ecosystems discussed in this paper include Axelrod’s iterated prisoner’s dilemma game [5], which can serve as a sort of E. coli of ecosystems, and biological ecosystems, which are familiar enough to serve as a point of reference for the rest. Others discussed are Lenat’s EURISKO program [III,6], political ecosystems, and what will here be termed direct and indirect market ecosystems. Markets are the central theme-other ecosystems are compared to markets, and markets themselves are generalized from existing human systems to proposed computational systems.
2. Evolution in ecosystems
Evolution proceeds by the variation and selection of replicators. The most familiar example, of course, is biological evolution, in which genes are the replicators [7,8], mutation is the variation mechanism, and a variety of environmental pressures (predation, parasitism, competition for scarce resources) act as selection mechanisms. The following will explore a variety of other ecosystems, the nature of their replicators, and the nature of their processes of variation and selection.
2.1. Ecosystems
Ecosystems provide contexts for evolution in two distinct senses. First, the ecosystem’s replicators evolve in response to unchanging aspects of their environment such as climate and physical principles. Second, the replicators interact (through predation, competition, cooperation, and so forth), with each replicator providing part of the context for others. When replicators respond to external selective pressure, but not to each other, the result is an evolutionary system, but not an ecosystem. In such a non-ecological system, the subtlety and sophistication of the selective pressures are fixed.
The environmental richness and complexity generated when evolving entities can interact arguably leads to increased richness and complexity of the resulting system: selective pressures are then themselves the results of evolution. Analyzing such a system may be difficult, however. With many complex, multi-way feedback loops possible, can one be confident in the stability or direction of the overall system? This depends on the nature of the forces and feedback.
The analysis of ecosystems frequently involves non-intuitive secondary and tertiary effects. The Axelrod tournament provides a simple example of these effects.
2.2. The Axelrod tournament
Robert Axelrod developed an ecosystem in which the entities interact in rounds of iterated prisoner’s dilemma games [5]. To understand it, one must first understand the dilemma itself. Instead of the traditional scenario of prisoners being interrogated, Hofstadter’s illustration with the following scenario seems more intuitive.
Two dealers arrange to trade items. Each dealer agrees to place his item in a bag and leave it at a designated place to be retrieved by the other dealer. The dilemma presents itself when each dealer considers how best to interact with the other-given that they are strangers, will not meet face to face for this exchange, and will never deal with each other in the future. As Hofstadter describes, each dealer reasons as follows:
”`If the [other] dealer brings a full bag, I’ll be better off having left an empty bag, because I’ll have gotten all that I wanted and given away nothing. If the dealer brings an empty bag, I’ll be better off having left an empty bag, because I’ll not have been cheated. I’ll have gained nothing but lost nothing either. Thus it seems that no matter what the dealer chooses to do, I’m better off leaving an empty bag. So I’ll leave an empty bag.’ . . .And so both of you, with your impeccable (or impeccable-seeming) logic, leave empty bags, and go away empty handed. How sad, for if you both had just cooperated, you could have each gained something you wanted to have. Does logic prevent cooperation? This is the issue of the Prisoner’s Dilemma.” [emphasis in the original] [9]
The underlying strategic situation can be made precise in the following fashion: In a single prisoner’s dilemma interaction, two players each choose between moves (termed cooperate and defect) in ignorance of the other’s choice. If both cooperate, both are rewarded (in Axelrod’s case, with a payoff of 3 points). If one cooperates and the other defects, the defector receives an even greater reward (5 points), while the cooperator receives nothing (0 points). If both defect, both are punished (by receiving only 1 point).
In a single move, each player has an incentive to defect regardless of the other player’s move, but double-cooperation is better than double-defection. Overall, pairs of players that cooperate earn higher scores than those that do not.
In an iterated prisoner’s dilemma game, two players go through a long series of moves, and can base their actions on the history of play. When one expects (and hopes for) further transactions with the other party, simple defection no longer seems as attractive. Indeed, by running a computer tournament, Axelrod showed that the logic of an iterated prisoner’s dilemma actually fosters cooperation.
Robert Axelrod ran a Computer Prisoner’s Dilemma Tournament based on the above rules. A diverse group of game theorists were invited to submit programs to play against each other in a round-robin of games, each averaging 200 single moves. After the first tournament, Axelrod circulated the results-including the nature of the winning program, judged by cumulative points-and solicited entries for a second tournament.
Axelrod’s pair of tournaments may be described as a simple evolutionary ecosystem. The replicators were the programs themselves (or the strategies those programs embody), the variation mechanism was human ingenuity (since programs were modified between tournaments), and the selection criterion during a tournament was simply the number of points earned. Programs interacted with each other in an environment imposing certain rules, and their success depended on each others’ behavior. Further, Axelrod went on to simulate the population dynamics of a set of programs, given the assumption that points earned determined the “population density” of that program in the next time period.
In both tournaments a very simple program won. That program was TIT FOR TAT, submitted by psychologist Anatol Rapoport. In the population dynamics simulation, the success of TIT FOR TAT was even more pronounced. Analyzing TIT FOR TAT’s success can suggest how to analyze other ecosystems.
2.2.1. The triumph of TIT FOR TAT
All sorts of strategies were submitted, including many which used complex reasoning based on past interactions, and one which responded randomly. The success of a strategy depended on whether it was:
- Nice-never defected first,
- Retaliatory-responded to defection with defection (thereby punishing defectors), and
- Forgiving-eventually stopped defecting in response to cooperation.
TIT FOR TAT is the simplest example of a nice, retaliatory, and forgiving strategy. It cooperates on the first move and then does whatever the opposing player did on the previous move.
Other strategies can be classified according to which of the above traits they lack. A strategy which initiates a defection (and thereby is not nice) may be termed a con man, since it is trying to gain at the expense of (and with the foolish cooperation of) its opponent-the simplest con man always defects. A nice strategy which does not defect in response to a defection (and thereby is not retaliatory) may be termed a sucker, since it can be taken advantage of by con men.
Con men have an advantage over TIT FOR TAT in that they can fully exploit suckers, while TIT FOR TAT only cooperates with them. Given the mix of strategies submitted to Axelrod’s tournaments, TIT FOR TAT won both. A con man strategy could have won, however, had the initial population included enough suckers. Since con men could have won in this case, how can one claim that TIT FOR TAT is fundamentally more viable than con men? Axelrod’s population dynamics simulation helps answer this question.
3. Evolutionarily stable strategies
In the population dynamics simulations, a population number is associated with each strategy, to indicate how many “organisms” in the overall population are following the strategy. In each generation, the score received by an organism is the score it would receive in playing a series of one-on-one games with every organism in a representative sample of the total pop- ulation. At the end of each generation, the total score accumulated by organisms using a given strategy determines how many organisms of that type will exist in the next generation. (A process of this sort-in which success in one round determines influence or existence in the next-distinguishes evolutionary game theory from conventional game theory. Evolutionary game theory need make no assumptions about motives or values, though it is natural to think in terms of a “survival motive” which generates a “success motive”.)
As Figure 2 shows, in a population dominated by suckers, a small population of con men have a great advantage, rising to temporary dominance. But in doing so, they drive down the population of suckers and so lose their advantage; they are then driven to extinction by TIT FOR TAT. As shown in the diagram, an environment with enough TIT FOR TAT players to fight off an invasion of con men can support a stable population of suckers.
In this ecosystem, TIT FOR TAT can be termed an evolutionarily stable strategy, or ESS. An ESS is a strategy which, given that it dominates an ecology, cannot be invaded by any other strategy [10,7]. In Maynard Smith’s terminology, “ESS” refers to a specific detailed strategy (such as TIT FOR TAT); here, the term will refer to general classes of strategies that share basic characteristics, such as being “nice and retaliatory”. The rules governing a given ecology determine the success of different strategic characteristics, and therefore the ESS.
As shown, suckers are not an ESS in Axelrod’s system because they can be invaded by con men. Con men are not an ESS except in a trivial sense-a population consisting purely of con men cannot be invaded by a small, scattered group of TIT FOR TAT players. A small but significant number of invaders, however, can cooperate, expand, and completely replace a population of con men. A population dominated by any strategy that is both nice and sufficiently retaliatory cannot be invaded by any strategy that is not. Any population dominated by a strategy that is not both nice and sufficiently retaliatory can be invaded. Therefore, the ESS of the Axelrod tournament is to be nice and retaliatory.
A single population-dynamics process can be described as an ecosystem, but not as an evolutionary ecosystem, since there is no source of variation. Axelrod’s series of two tournaments included variation from one to the next, and hence qualifies. To transform it into a better example of an evolutionary ecosystem, imagine a continuing tournament open to outside contestants able to create new strategies and introduce them in small numbers. In any such open, evolving ecosystem, given no special restrictions on allowable variations, one should expect the ecosystem to become populated primarily by an ESS. The properties of such an ESS will often indicate emergent properties of the system. For example, in any open Axelrod ecosystem most moves will be cooperative.
The above discussion of Axelrod’s system benefits from hindsight. The original game-theory experts who submitted the original strategies knew the rules, and those who submitted strategies for the second tournament even had the benefit of a bit of hindsight from the first tournament. Nevertheless, in both cases most of the strategies submitted were not nice, and so were not ESSs. The analyses which follow cover much more complex ecosystems, in which the nature of strategies and payoffs are much more subtle.
As a result, many of the points made in the rest of this paper are not settled conclusions, but merely initial hypotheses to be tested. The best testing methodology is that used by Axelrod: run a system and open it to outside contributors. The goal is to understand what properties of a computational ecosystem will result in useful system behavior.
4. Biological and market ecosystems
This section compares biological and idealized market ecosystems, focusing on the differing evolutionarily stable strategies they foster. Idealized markets, as defined here, are computationally-inspired abstractions having parallels with human markets but omitting certain of their complexities and problems. The idea of a computational market is not developed in detail in this paper; see [I,II] for a more concrete discussion.
4.1. Rules of the games
The above analysis of Axelrod’s ecosystem began with an examination of the rules of the game. These rules are the constraints within which organisms of that ecosystem must operate. The only fundamental constraint on either biological or human market ecosystems is physical law: any action not forbidden by physical law is in theory possible for players in either ecosystem. However, in order to analyze these ecosystems, it is useful to consider idealized versions in which players operate under additional constraints.
4.1.1. Foundations of biological ecosystems
An example of a physical constraint in biological ecosystems is the conservation of mass and energy. Among animals, the critical resources-biomass and free energy-are downwards conserved: they can be transferred and reduced by the transactions animals are capable of, but not increased. Plants can obtain these resources by photosynthesis; access to sunlight and land area are among their critical limited resources. Biomass and free energy are needed to sustain activity, and can be transferred by predation.
Other constraints in biology (at least if evolutionary history is any guide) include the primary use of proteins for construction of molecular machinery and the use of ribosomes programmed by nucleic acids for their manufacture. These constraints (while not essential to the present discussion) have been shown to limit severely the materials and processes available to biological systems [11,12].
4.1.2. Foundations of idealized markets
In the attempt to characterize an idealized biological ecosystem, it is fortunate that the boundary between living and non-living systems is still fairly clear. In contrast, human markets exist in the context of governmental activity and crime-this makes idealization a larger and riskier task. The following will analyze idealized market ecosystems with simple foundational rules of sorts that can be rigorously enforced in a computational context. This analysis draws heavily on analogies with human markets, while omitting certain difficulties that are excluded by the idealization. Section 6.2 will build on the concept of an idealized market, describing a direct market ecosystem with further differences from human markets; again, these differences are inspired by the possibilities of computational systems.
The basic rules of human markets are typically encoded in legal systems and enforced by attempting to catch and punish violators. In a computational setting, these rules can be enforced as unbreakable “physical” laws. In particular, rights of property (or ownership) can be implemented through encapsulation [I,IV,V]; unforgeable currency and trademarks can be implemented through public key systems [13,14]. The computational entities within such a system could no more steal than human entities can travel faster than light. These abilities can provide the foundations for idealized markets.
An idealized market can contain a great variety of resources, analogous to items ranging from land to airplanes to currency tokens. These resources can be owned by individual entities or groups. No one may take such resources from their owner, but an owner may voluntarily transfer them to any other party. When this occurs in a reciprocal exchange, we refer to the transaction as a trade. Exchanges cannot increase the quantity of any resource-resources are locally conserved across transfers. Productive activity, however, can increase supplies of many resources.
By the rules of the game, anyone may produce new airplanes. Were this the case for currency tokens, however, they would be useless as currency. The rules of an idealized market therefore permit manufacture of a given currency only by a corresponding mint [14]. The effects of minting and introducing new currencies into a market ecosystem are complex [15,16], and are ignored in this paper. The following assumes a currency which is both locally and globally conserved.
A key difference between biological and idealized market ecosystems is the ability to establish and use unforgeable identities. Nature abounds in examples of mimicry and in imperfect attempts to avoid being mimicked [17]. A right to trademark is here defined to be one of the rules of idealized markets. Any entity may establish a new trademarked identity and attach it to that entity’s product or place of business. No entity may do this with another’s trademark.
4.1.3. Variation and selection
In biology, the replicators are genes, and the variation mechanism is relatively random mutation of an organism’s genetic code-its genotype. This does not mean biological variation is random. An organism’s phenotype-its body structure, abilities, and so forth-determines its success [18]. An organism’s phenotype is decoded from its genotype through a complex translation process. The encoding of a phenotype determines what other phenotypes are reachable by small mutations of a genotype. Therefore this encoding itself can embody heuristics for plausible phenotypic mutations (for example, leg-lengthening mutations interact with the heuristic rule of embryonic development that says, in effect, “do the same to both sides”). As explained in [III], AM and EURISKO employ computational embodiments of this principle (as do genetic algorithms in classifier systems [19]). Nevertheless, biological variation is essentially short-sighted, limited to incremental changes.
The variation and selection mechanisms of market ecosystems are less constrained to local optimization or hill climbing than are those of biological ecosystems. In biological evolution, temporary changes for the worse (temporary travel downhill) will typically lead to extinction through competition from organisms that have not gone downhill. This, together with the small steps possible through typical mutations, greatly limits the ability to reach distant peaks, however high they may be.
Variation in the human marketplace (as in the computational markets described below) frequently results from invention and design by people (or other entities able to plan ahead) who can design coordinated sets of non-incremental changes. Investors in a market (e.g., venture capital firms, in the human market) can take into account arguments for anticipating future success despite present failure, and invest in crossing a valley to get to a higher hill. Biological variation cannot take such arguments into account. By rewarding successful investors, markets select for entities that can facilitate these large jumps. Design and evolution are sometimes presented as mutually exclusive principles, but market ecosystems make use of both.
4.1.4. Success metrics
Success (or “fitness”) in an evolutionary process is sometimes defined in terms of long-term survival, but doing so would give little help in analyzing the short term. Also, the goal here is to use evolutionary reasoning to predict the nature of an ecosystem, not to determine what types of creatures will be around at some distant time. For these purposes, a useful criterion of a replicator’s success is the magnitude of its ability to affect its environment. This is itself hard to measure, giving reason to seek a metric which is positively correlated with this ability.
In biology, control of biomass and free energy correlates with ability to engage in biological activity. In a market ecosystem, an entity’s net worth is the measure of its resources, and hence a rough measure of its potential ability to engage in market activity. The following analyzes strategies for achieving these kinds of success.
4.2. ESSs in biological ecosystems
To survive, animals must eat animals or plants; this happens most often though predation. (Here entities which are eaten, whether animals or plants, are termed “prey”.) This is not a synergistic or symbiotic process-the incentives are not toward cooperation between predator and prey. If they were, the participants would both try to facilitate the predatory transaction.
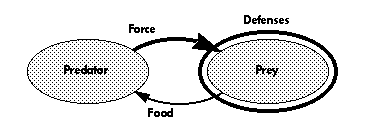
Instead, the incentives lead to an arms race in which predators develop better “teeth” and prey develop better “armor”. “Teeth” here refers to any mechanism for facilitating predation, such as a cheetah’s legs or a dog’s nose. “Armor” here refers to any mechanism for avoiding being preyed upon, such as a gazelle’s legs or a skunk’s scent. An animal without effective “teeth” would starve, and one without effective “armor” would rarely live long enough to reproduce.
Plants are seldom predators, but are often prey. As prey, they develop spines, grit to wear down teeth, and poisons (many are carcinogenic [20]). This has spurred another arms race in which animals have developed large, grinding molars and biochemically complex livers to deal with poisons. Plants compete for light in yet another arms race. This has led to the growth of trees which invest in huge wooden columns for the sake of tallness, to intercept their neighbors’ light. Efficient, cooperating plants would instead cover the Earth with grassy or mossy growth; their energy would be stored, not in inert wood, but in sugar, starch, oil, or some other metabolizable reserve.
Predation is a negative-sum relationship: one of the participants benefits, but only at a greater cost to the other. Biological competition is roughly zero-sum in the short term, but spurs a wasteful negative-sum arms race over the long term. Of course, there are many examples of symbiotic, positive sum relationships in biology, but the basic ESS of biology is one of “teeth and armor”.
4.3. ESSs in idealized market ecosystems
In order to sustain activity, players in the idealized market must obtain valuable resources, or goods. They can do so through the equivalent of solitary prospecting and manufacture, but the limited competence of any one entity will favor obtaining goods from others-that is, division of labor. Since the rules of the idealized market make it impossible to seize goods by force, one entity can obtain another’s goods only by inducing it to engage in a voluntary transaction. An entity which simply gives away goods would steadily lose resources and influence compared to one which does not; such a strategy would not be an ESS. Therefore, the strategy of simply accumulating donated gifts would also not be an ESS.
To induce “gifts”, an entity must offer something in exchange. For both sides to want to trade, each must value the goods received more than the goods given. Pair-wise barter deals of immediate mutual benefit are hard to find, and would yield only part of the full potential benefit of trade. Large multi-way deals would yield the full benefit, but are difficult to negotiate. Trade of goods for currency is therefore the expected dominant pattern; currency makes it easier for the equivalent of large multi-way barter deals to occur through separate pair-wise trades.
Each trade in a market can be seen as moving the system toward a condition (one of many possible) in which no transaction that will make both parties better off remains to be done (a condition known as Pareto optimality). Each trade can be seen as a hill-climbing step. Pair-wise barter amounts to hill-climbing across a rough terrain with few available moves; trade in a system with currency and prices amounts to hill-climbing across a smoother terrain with many available moves.
In a trade of goods for currency, the player paying currency in exchange for goods we term a consumer and the one selling goods in exchange for currency we term a producer. A set of producers competing to provide the same (or very similar) goods we term an industry.
Consumer-producer relationships can be contrasted to predator-prey relationships. Producers, unlike prey, will voluntarily seek out those who want to consume what they have, using advertising, distribution networks, and so forth. Consumers, less surprisingly, will seek out producers (in human markets, they do so by reading advertising, traveling to stores, and so forth). The symbiotic nature of this interaction is shown by the interest each side has in facilitating it. Since trade typically increases the viability of both participants, it also raises the viability of the pair considered together as an entity.
There are many negative-sum pair-wise relationships in even an ideal marketplace-the most common is competition among producers in the same industry. In judging the nature of the market as a whole, however, it is important to note that when producers compete, each is competing to do a better job of cooperating with the rest of the world, of attracting consumers into beneficial trade relationships.
In the absence of perfectly-effective rules to prevent it (which seem difficult to define, even in the computational domain), markets will suffer from fraud. A fraudulent transaction occurs when a producer induces a consumer to pay for an undesired good under false pretenses.
It is worth distinguishing fraudulent trades from those in which (in light of later information) a different alternative would have yielded a better product or a better price. Non-optimal trades are universal, given imperfect knowledge (which will be ubiquitous in computational markets), but this observation would argue against the use of market mechanisms only if someone could find a better way to use imperfect knowledge. Unlike fraudulent trades, non-optimal trades are still symbiotic; they merely fall short of an imagined perfection.
The possibility of fraud, together with the difference in quality among available deals, creates an incentive for consumer wariness. Wary consumers will in turn create an incentive for producers to avoid fraud, and for them to offer high quality (though not necessarily optimal) deals. The resulting ESS is to be “productive and wary”-wary as a consumer and productive and honest as a producer-for many of the same reasons that “nice and retaliatory” is Axelrod’s ESS. Given a variety of strategies in a brand-new market ecosystem, one can expect that fraudulent producer strategies will initially profit at the expense of non-wary consumer strategies. As a result, wary consumers will grow in importance, driving out fraudulent producer strategies. These considerations will even drive out honest producer strategies which are noticeably less productive than their competitors. At a finer level of resolution, of course, there will be as many detailed strategies for being productive and wary as there are niches for entities in the market.
How can a consumer be effectively wary? The producer-consumer relationship is similar to an iterated prisoner’s dilemma. If a producer fraudulently sells a worthless product, he is “defecting” on the arrangement. A wary consumer must take the trouble to notice this defection in order to retaliate (for example, by doing business elsewhere and warning others away). Checking for a defection can be expensive, however, and consumers are frequently in non-iterated situations. Reputation agencies like Consumer Reports can lower the cost of wariness and make it more effective by putting the producer in an iterated situation with the community as a whole (see the discussion of reputation agents in [I]). Trademarking of ser- vices and products enables producers to establish valuable reputations. The lack of this mechanism in biology [17] contributes to the relative sparseness of symbiosis there.
4.4. Food webs and trade webs
Biological and market ecosystems both contain a mixture of symbiotic and negative-sum relationships. This paper argues that biological ecosystems involve more predation, while idealized market ecosystems involve more symbiosis. Indeed, one can make a case that this is so even for human market ecosystems-that biological ecosystems are, overall, dominated by predation, while market ecosystems are, overall, dominated by symbiosis.
In human markets (as in idealized markets) producers within an industry compete, but chains of symbiotic trade connect industry to industry. Competition in biology likewise occurs most often among those occupying the same niche, but here, it is predation that connects from niche to niche. Because of the lack of reputations and trademarks, symbiosis in biology occurs most often in situations where the “players” find themselves in a highly-iterated game. In the extreme, the symbiotic system itself becomes so tightly woven that it is considered a single organism-as with lichens composed of fungi and algae, or animals composed of eukaryotic cells containing mitochondria. Predation, of course, links one symbiotic island to the next.
Ecology textbooks show networks of predator-prey relationships-called food webs-because they are important to understanding ecosystems; “symbiosis webs” have found no comparable role. Economics textbooks show networks of trading relationships circling the globe; networks of predatory or negative-sum relationships have found no comparable role. (Even criminal networks typically form cooperative “black markets”.) One cannot prove the absence of such spanning symbiotic webs in biology, or of negative-sum webs in the market; these systems are too complicated for any such proof. Instead, the argument here is evolutionary: that the concepts which come to dominate an evolved scientific field tend to reflect the phenomena which are actually relevant for understanding its subject matter.
4.5. Is this picture surprising?
Nature is commonly viewed as harmonious and human markets as full of strife, yet the above comparison suggests the opposite. The psychological prominence of unusual phenomena may explain the apparent inversion of the common view. Symbiosis stands out in biology: we have all heard of the unusual relationship between crocodiles and the birds that pluck their parasites, but one hears less about the more common kind of relationship between crocodiles and each of the many animals they eat. Nor, in considering those birds, is one apt to dwell on the predatory relationship of the parasites to the crocodile or of the birds to the parasites. Symbiosis is unusual and interesting; predation is common and boring.
Similarly, fraud and criminality stand out in markets. Newspapers report major instances of fraud and embezzlement, but pay little attention to each day’s massive turnover of routinely satisfactory cereal, soap, and gasoline in retail trade. Crime is unusual and interesting; trade is common and boring.
Psychological research indicates that human thought is subject to a systematic bias: vivid and interesting instances are more easily remembered, and easily remembered instances are thought to be more common [21]). Further, the press (and executives) like to describe peaceful competition for customer favor as if it were mortal combat, complete with wounds and rolling heads: again, vividness wins out. These factors go far to explain the common view of market and biological ecosystems.
For contrast, imagine that symbiosis were as fundamental to biology as it is to markets. Crocodiles would not merely have birds to pick their teeth, symbiotic bacteria in their guts, and the like; they would have symbiotes to provide them with orthodontia and tooth crowns, to say nothing of oral surgery, heart surgery, and kidney transplants, as well as shoes, clothing, transportation, housing, entertainment, telecommunications, massage, and psychiatric care.
Likewise, imagine that predation were as fundamental to markets as it is to biology. Instead of confronting occasional incidents of theft in a background of trade, one would be surrounded by neighbors who had stolen their cars from dealers who had mounted an armed assault on factories in Detroit, which in turn had grabbed their parts and equipment by pillaging job-shops in the surrounding countryside. So-called “hostile corporate takeovers” would involve, not purchase of shares of ownership from willing stockholders, but a sudden invasion of offices by an armed gang.
Biological ecosystems have evolved creatures and environments of great beauty and complexity, and they exhibit a grand spontaneous order, but that order is quite different from the synergistic, symbiotic order of the market. If the aim in building computational ecosystems were to maximize their beauty and complexity, biology might be an excellent model. Given the goal of building a computational ecosystem which will organize itself to solve problems, however, one should seek a system that fosters the cooperative use of specialized knowledge and abilities. Market ecosystems seem better suited to this.
4.6. Are markets just biological?
It might be objected that the mechanisms which facilitate widespread symbiosis in market ecosystems are achievable within the rules of biological ecosystems. After all, these rules do not forbid organisms from pooling their resources to defend against predators or from establishing reputation and trademark systems. Indeed, this has been done. Through such institutions as laws, courts, banks, and trademarks, talking primates have taken their species through the transition from “nature, red in tooth and claw” to an industrial civilization spanning a planet. Though this has been achieved within the rules of biology, biological rules do not deserve the credit, any more than a machine language deserves credit for the virtues of Lisp.
This comparison of biological and market ecosystems suggests some of the strength of markets as a model for computation. The following examines a simpler computational ecosystem and considers whether market mechanisms would be useful in similar systems.
5. EURISKO and markets
Lenat’s EURISKO system [6] may be viewed as an ecosystem in which the replicators are interacting, evolving heuristics-that is, evolving, computational rules of thumb. Two kinds of heuristics populate EURISKO: object-level heuristics whose subject domain is some topic to be explored (such as war games or three-dimensional VLSI), and meta-heuristics whose subject domain is heuristics. Variation occurs as meta-heuristics create new heuristics from old ones via mutation, and selection occurs as meta-heuristics judge and determine the “interestingness” of heuristics (a numeric value associated with a heuristic). This quantity determines allocation of processing resources, so heuristics compete for survival and influence based on their degree of “interestingness”.
To apply EURISKO to set theory, for example, one would start it with a set of object-level heuristics representing basic concepts of set theory (such as set equality and union), meta-heuristics for creating plausible new concepts out of old ones (e.g., by removing a conjunct from a predicate to weaken it), and meta-heuristics that attempt to capture a sense of what is mathematically interesting (such as an unexpected coincidence). EURISKO’s predecessor, AM, started with exactly this, and was able to discover (and judge interesting) in turn: whole numbers, addition, multiplication, factorization, primality, and Goldbach’s conjecture.
(There has been some controversy over the sense in which AM can be said to have discovered these concepts, and whether it is a reproducible result. For a discussion of these issues, see [III]. Also, note that many of these results have been reproduced by Ken Haase’s EURISKO-like program, CYRANO [22].)
In AM, meta-heuristics mutated and judged object-level-heuristics, but did not themselves evolve under each others’ influence. This was changed in EURISKO: here both kinds of heuristics exist at the same level of the system and can operate on each other freely. This enabled the mechanisms of variation (including the representation language) and the selective pressures to evolve and adapt with the rest of the system.
5.1. Parasitic loops
During a run of EURISKO, however, one meta-heuristic rose to the maximum interestingness value merely by listing itself as a creator of whatever heuristics were judged interesting. As a “creator” of such interesting heuristics, it was itself judged interesting. Lenat reports that EURISKO has, when run for long periods, consistently invented ways to enter infinite loops of one sort or another. This problem may be viewed as the evolution of parasites, of systems that consume resources while returning nothing of value.
Lenat has limited this problem by hand-tuning sets of meta-heuristics, and by placing certain meta-heuristics on a frozen meta-level protected from evolutionary modification. But doing this can solve the problem of parasitism only if all entities which assign interestingness are placed in this frozen meta-level. A major part of the system is thus unable to evolve beyond its initial design, and hence unable to adapt to unforeseen changes within the system. This type of solution loses much of the flexibility sought in the move from AM to EURISKO.
“Interestingness” is a standard of value which can be used to claim system resources; if evolving meta-heuristics are allowed to assert value-and hence to generate claims from nothing-then parasites can evolve. If direct self-reward is forbidden, jointly self-rewarding “conspiracies” would spontaneously arise. For example, if a heuristic is consistently being judged interesting by a particular meta-heuristic, it is an ESS for it to discover some way to feed some of the resulting resources back to that meta-heuristic, that is, to find a way to pay a “kickback” to a judge (not to influence the judge in its favor, but to increase a favorable judge’s influence). This problem can also be seen as a “tragedy of the commons” [23]: processing resources are the commons, and since the cost of using them (in terms of forgone alternative uses, etc.) is borne almost exclusively by others, each entity has an incentive to gobble resources wantonly.
5.2. Conservation laws
This dilemma can be avoided by imposing restrictions on value-assertion at a simple, foundational level, rather than restricting valuation to a static set of complex heuristics. How can this be accomplished? Biology and markets both have locally-conserved quantities (matter, energy, currency) that are measures of success, and both systems have steadily generated new, genuinely interesting results. Sterile self-reinforcement cannot lead to success, because it cannot bring in resources. This principle can be applied to EURISKO-like systems.
An attractive approach is reward based on a locally-conserved currency, used to pay for services and computational resources. This inhibits parasitism through stable foundations which themselves embody no knowledge of heuristics (other than this argument). In such a system, a heuristic must pay for processing and for services provided by other heuristics. Non-productive loops of mutually-rewarding heuristics then go broke, since (by conservation of currency) a group of heuristics can only gain net funds by receiving them from a solvent entity outside the group-an entity that, presumably, either receives or expects to receive some valuable service. A productive entity may unwittingly support an unproductive process, but competitive pressures will help weed out this behavior.
The elimination of unsupported, non-productive entities by letting them go broke is a robust result of a foundational constraint, not a chancy result of hand-tuned heuristics. It achieves its robustness and universality in the same manner as many physical principles: it relies on a conservation law, and hence is independent of subsystem boundaries and system structure.
5.3. A market-based EURISKO?
Market mechanisms suggest how a EURISKO-like system could operate without level boundaries or protected sets of supervisory heuristics. In a system of this sort, when a heuristic is invoked it charges the user enough to pay the costs of providing service, plus a royalty that rewards the heuristic’s creators. As users learn to make discriminating choices, heuristics will compete to maximize their performance per unit of system resources consumed. Meta-heuristics that create new heuristics will earn royalties from their creations to the extent that these creations prove useful. Where several heuristics are responsible for creating a given heuristic, they can be viewed as its “stockholders”, splitting royalties (or dividends) according to a prior contractual agreement.
Rules for negotiating the terms of such agreements can themselves evolve; the proper division of rewards will itself be rewarded, since it will lead to the evolution of better subsystems. Being able to evolve better division of rewards is important for a capable learning system (see the discussion of genetic algorithms and connectionism in Appendix II of [I]).
The above has outlined how money circulates among heuristics, and how it is ultimately used to pay for processing resources. Where does this flow of money originate? The next section answers this first by re-introducing a protected meta-level, though one that avoids the above problems, and then by explaining how to remove this meta-level as well.
5.4. External funders and open systems
In a closed, market-based EURISKO-like system, heuristics pay for the storage space and processor time they use; the funds collected are then recycled to fund computation. If entities external to the economic system control the re-introduction of funds, then the heuristics within the system will be selected for their effectiveness in solving the problem of meeting the criteria for funds allocation. Ultimately, these criteria represent the problem being posed to the system; they could be simple contingent rewards for solving problems.
The funding agency is outside the system, and so not subject to heuristic evolution. It might seem equivalent to Lenat’s protected meta-level, but, unlike EURISKO, a system of this sort can contain a fully-capable set of evolving meta-heuristics. The external funders reward only end results; meta-heuristics inside the system can act as internal investors, accelerating the adaptation of the system to the externally-defined goals. Investors and the activities in which they invest all participate in the same one-level market system. Use of this sort of meta-level avoids freezing the criteria for judging intermediate results, or for judging the judges of intermediate results (this resembles suggestions for funding scientific research [24]).
The unobjectionable role of the external funding agency is clear when the system is considered as part of a broader economy, in which external human users provide the funding and hence the feedback. The evolution of programs is ultimately guided by human judgment of what constitutes good performance [VI]; in a market-based, EURISKO-like system, the “super- visory” heuristics that judge other heuristics would themselves be judged by people. This supervisory position entails no special privilege; it results from their role as entities directly funded by users. The EURISKO experience may also be viewed in this light. Lenat’s protected meta-heuristics were not really immune from evolution: Lenat himself varied and selected them with respect to the behaviors they encouraged, and allocated physical processors to those versions of EURISKO which he judged more promising.
In a distributed system consisting of EURISKO-like nodes subcontracting to each other, the external funding agency of any one node can consist of other nodes (of course, this principle does not require separate machines). In an open computational market-one using real dollars and connected to the human market-participating humans may be thought of as the ultimate meta-heuristics. They will be the ultimate source and drain for the flow of funds in the system, and will be the ultimate source of variation (at least initially). However, they are in no sense protected meta-heuristics. The flow of real money, and the provision of actually useful software services, will provide an incentive for humans to work to make the system more useful, and for them to buy the useful services being offered (see “Agoric Systems in the Large” in [I]).
6. Memes and markets: direct and indirect market ecosystems
Human cultures evolve. Their replicators are any of the information patterns which make up a culture, and which spread (with variation) from human to human via imitation. By analogy with genes, these replicators are known as memes [7]; they include ideas, beliefs, habits, morals, fashions, designs, techniques, jokes, and more. Any pattern which can spread via imitation is a meme, even if its human host cannot articulate it or is unaware of its existence.
It is important to recognize that the replicators of human culture are memes, not people. The lack of this distinction has led to the unfortunate confusion called “social darwinism”. Our ability to change our minds allows cultural evolution to proceed not by selection of humans, but, as Karl Popper says, by “letting our theories die in our stead” [4].
Recognition of the evolutionary nature of human culture has inspired computational proposals for aiding the spread of memes among humans [25,26] and for establishing a memetic ecosystem among software entities [VII]. The memes making up human culture are diverse, as are their variation and selection mechanisms. Rather than studying human culture as a single, generic kind of ecosystem, it makes more sense to view it as composed of several interacting memetic ecosystems.
For example, Karl Popper describes science in evolutionary terms [4]. The replicators of science are theories, and their evolution proceeds through a process of conjecture and refutation, that is, variation and selection. The selection criteria include the requirement that a theory be both falsifiable and not actually falsified. (Falsifiable means that if it were false, it could be refuted by experiment.) In science only falsifiable but true theories are ESSs-any theory which is false either can be refuted, or is not falsifiable, and so is subject to rejection. In memetic systems whose replicators are theories, but which apply other selection criteria, theories which are not true may nevertheless be ESSs. Idealizations of scientific inquiry have also inspired computational ideas and systems [27,28].
6.1. Market memes and the indirect market
In this paper, the memetic systems of interest are those that shape activities in markets, here called market memes. They include ideas that shape strategies for production, organization, marketing, investment, and much more. Market memes can be embodied in individuals or in groups such as firms, but their mechanisms of selection are indirect, working through the human brain.
Money flows not to successful market memes, but to their hosts. No matter how much money it brings in, a meme is unable to rent more brain space-indeed, it cannot even protect itself from being displaced. Entities directly interacting with an ideal market can own assets which cannot be seized; memes can own no such assets.
Market memes can replicate by spreading from human to human, but for some, this process is difficult. Complex market memes, such as business management skills or organizational patterns, are hard to communicate without introducing great variation. Biological systems can generate and test many small variations of a genetic pattern, replicating the more successful, but human markets can seldom do the same with organizations.
Meta-market memes are memes responsible for generating new market memes; an example would be an idea for how to educate better entrepreneurs. When their results are successful, however, no reward reliably propagates back to the memes responsible. Since meta-market memes do not receive credit for their efforts, people are led to underinvest in them.
Thus, market memes are able neither to benefit directly from their own successes, nor (in general) to replicate and pass on their successful characteristics. These defects in the system for creating, expanding, and replicating market memes make their evolution a slow and clumsy process. Successful practices are recognized and imitated, but quite imperfectly.
Although institutions such as patents, trade secrets, and copyrights attempt to strengthen feedback loops, there is only an indirect coupling between market forces and the replicators of the human market-this system thus constitutes what has here been called an indirect market. In software, however, it seems possible to achieve a direct market-an ecosystem in which the replicators that dominate the evolutionary process are directly rewarded by market success.
6.2. Direct market ecosystems
In a direct market implemented in software, a successful heuristic or strategy can directly acquire more processing power and can replicate itself with small variations if it chooses. In these ways, a direct market resembles the biological ecosystem more than it does human markets. In addition, meta-heuristics can generate new software entities from old ones (that give access to the requisite information) by plausible mutation and recombination of the patterns that embody them. The generation of new entities will generally occur only after the participants have negotiated a division of any later rewards (a portion of their shares will, in turn, propagate back to their own creators). These mechanisms directly reward (and thereby encourage) “meta-market” activities, such as inventing new forms of business.
Direct markets have other advantages over human markets. In human markets rules against theft and extortion are enforced imperfectly through mechanisms such as police, courts, and jails. In software, however, these rules can be like “laws of physics”. Human markets are plagued by negative externalities (such as air pollution) resulting from the unowned and non-local nature of many common resources (such as air). In software, it seems that these problems can be largely avoided. The basic resources of computation-processor time, memory space, and communications bandwidth-can be allocated without negative externalities [II]. No commons seem needed in computational ecosystems; computational environments need have no analogues of air, water, lines of sight, or rainforests.
The discussion thus far has assumed that computational markets are “idealized markets”, in the sense introduced in Section 4.1.2, operating under only simple, foundational rules, preventing non-voluntary transactions analogous to theft. Human markets, however, operate under a wider range of less rigorously enforced rules, imposed by a variety of legal and regulatory institutions. The next section examines whether such institutions might be of use in computational markets.
7. Computational legal systems and markets
Like human markets, direct computational markets will have many problems. Computational markets are enough like human societies that it is worth examining mechanisms-such as law and regulation-used by human societies to try to deal with these problems. However, these analogies must be used with care-there are also many differences between human and computational markets. For example, in proposed computational markets:
- No negative externalities exist in basic resources (processor, memory, communications), hence there are no problems analogous to pollution.
- Replicators directly own resources, making the evolutionary process more like “social darwinism” than like the actual evolution of human societies.
- Participants are not people (or even animate), hence they are not hurt when they go broke.
- Object encapsulation prevents force absolutely, hence there is no “who will watch the watchers” problem.
- Only information services are sold, hence there are no depletable inventories of manufactured goods.
Given all these differences, one should not demand that government-like systems proposed for computation be closely patterned on those evolved by human societies. A more appropriate use of the social model is as a source of ideas and analogies, and ideas need not be workable in society to be worth considering in computation. Since computer science has already examined centralized forms of organizations, a promising direction to explore is the other extreme, that of highly decentralized models.
7.1. Remaining problems of direct computational markets
Direct computational markets can be built so as to exclude theft and negative externalities; this leaves problems such as fraud, overall fluctuations (such as business cycles and depressions), monopolies, and provision of public goods (goods whose provision will benefit entities that do not purchase them, breaking the usual link between public benefit and producer reward). These problems are fundamentally different from the problem of theft, which can be eliminated in computation via simple local rules such as encapsulation. Eliminating any of the problems just mentioned requires the recognition of complex emergent phenomena:
- Fraud involves the non-delivery of promised value; its elimination would require (at least) understanding all possible representation languages in which these promises can be expressed, and recognition of the conditions defining the fulfillment and non-fulfillment of all promises.
- Overall fluctuations are typically measured in terms of economic aggregates such as GNP, which involves collecting considerable information about transactions and determining rules for aggregating them.
- Monopolies can only be recognized by first determining both what constitutes an industry and what constitutes an “anti-competitive” practice.
- Public goods situations can be recognized only if benefits can be recognized, along with the absence of ways to reward producers for them through normal market mechanisms.
An official fraud-deterring function must at least understand the “advertising” in the system, which is difficult in computation-every inter-object protocol constitutes a different sub-language, and in general, none is globally understood. As explained in Section 4.3, however, and in Section 5.3.3 of [I], computational markets can themselves deter types of fraud which local entities can recognize, just as they routinely judge the comparative values of different opportunities. For a workable system, it seems that the one essential anti-fraud law is also implementable-to prevent fraudulent use of another’s trademark.
In human markets, overall fluctuations of an economy (such as business cycles and depressions) have stimulated the creation of governmental institutions such as federal reserve banks and deficit spending; the rise of monopolies in certain industries has stimulated the creation of anti-trust laws. In both cases, there is controversy regarding whether the problems themselves are intrinsic to human markets or whether they result from political intervention [16,29,30,31,32]. Computational markets will be different enough from human markets that these problems may either be severe, or not occur at all. The game theory of these phenomena is so complex that a priori argument may be fruitless; an experimental methodology seems more promising. The simplest approach may be to build computational markets that lack any foundational mechanisms to prevent these problems, and then observe the results.
A public good is one that, if provided, benefits members of a group independently of whether those members have paid for it. Examples include national defense and residential streets. Consider the incentives of a potential contributor: “If I refuse to pay, the good may be provided anyway, and I will have gotten it for free. If I do pay, my contribution will be such a small fraction of the total that I will not significantly increase the amount of the good being provided, so I will refuse to pay.” (This is also known as the free-rider problem, because some entities can get a free ride on the efforts of others.) Thus, if left to the market, public goods will be underproduced, from the standpoint of overall benefit.
Many public goods problems can be avoided in a computational setting. Ingenuity can convert many seemingly public goods into marketable goods, thereby enabling market incentives to reward appropriate production. Examples include the “Dividend Algorithm” presented in [II], and the difference between selling information and selling information-based services explained in Section 6.2 of [I]. Nevertheless, for true public goods, the problem is intractable in a market framework. In the case of human society, a legal principle has been proposed to deal with this issue.
7.2. Public goods and “takings”
Richard Epstein has proposed [33] a legal principle derived from the “takings” clause of the U.S. Constitution, which grants to the federal government the power of eminent domain over private property. The takings clause limits forcible seizure of property, stating “. . .nor shall private property be taken for public use, without just compensation.” Epstein argues for the principle that any taking from an entity, including taxation, must be compensated by the return of benefits of equal or greater value. It may readily be seen that, where the taking is indeed of net benefit, full compensation (whether in money, goods, or services) will be possible. Where full compensation is quantitatively impossible, the net cost must exceed the net benefit-and the taking itself is therefore undesirable.
To apply this principle requires a complex evaluation of costs and benefits on a case-by-case basis. Epstein, as a legal scholar writing about human society, proposes the use of legal mechanisms (courts and evolved systems of law) presently unavailable in a computational setting. The closest equivalent of such mechanisms would comprise a complex set of heuristics-so complex that it would have to evolve, rather than be built into the computational foundations as a frozen set of rules. How might complex laws evolve in computation?
7.3. Political ecosystems
In human societies, legal systems and governmental activities provide a framework for the market. They can be seen as a meta-level with respect to market activity, but they are not protected from evolutionary forces; instead, they evolve within a political ecosystem with its own mechanisms for the variation and selection of laws and interventions.
In recent years, the tools of economic analysis have been applied to the evolution of policies within democratic political ecosystems [34,35]. This work defines vote and growth motives that parallel the well-known profit motive. All these motives have some claim to be motives to act in the public interest; all, in practice, have their flaws:
- The profit motive: do what people want, as shown by their willingness to pay for the result (but cheat customers, if your reputation won’t catch up with you).
- The vote motive: do what people want, as shown by their willingness to vote for you and your platform (but lie and sell out to special interests, if it will win votes).
- The growth motive: do what people want, as shown by their elected leaders’ willingness to expand your agency (but do not achieve goals too economically, or your budget will be cut).
In each case, evolutionary forces-not psychology-virtually guarantee behavior in accord with these motives: profitable businesses, vote-winning politicians, and growing agencies will (almost by definition) dominate their fields. Evolution selects for those that act in accord with these motives, whether or not they feel these motives, just as evolution selects for genes that act in accord with the reproduction motive, though genes have no minds or motives at all. And when genes build organisms with minds, those minds may feel a sex motive rather than a reproduction motive. In a like fashion, selection of individuals and ideas could, in a hypothetical world, evolve institutions led by public-spirited executives, politicians, and bureaucrats, all subjectively selfless, but all acting in accord with the profit, vote, and growth motives (if only to keep their positions of influence, to enable future good works).
Analysis of the vote motive shows how socially destructive policies can win elections [34,35], hence the idea of correcting computational markets with computational democracies should be approached warily, at best. Further, it is not immediately obvious how a computational democracy would work. If one were to substitute “one object, one vote” for “one person, one vote”, the result would be the immediate creation of vast numbers of otherwise useless voting-objects. One would prefer a system with a better incentive structure.
7.4. Meta-market ecosystems
Imagine a system in which computational objects can choose to operate in any one of a number of legal environments, and in which new legal environments can be created at any time. Since environments could be copies of other environments, they can replicate; since they can also vary and be selected, they can evolve. A measure of the evolutionary success of a legal environment is its level of use (objects can vote with their nonexistent feet); one should expect the behavior of evolved systems of this sort to be describable in terms of an “attractiveness motive”.
Something of this sort is seen in the human world. There are many human markets, each with its own set of rules, and each interacting and competing with the others. Stock and commodity exchanges, diversified corporations, and nations each employ a different set of rules governing their internal markets. In each case, entities with different internal markets are able to trade and compete with each other. Factoring out the other dimensions, these amount to a system of competing legal systems.
Each of these legal systems would have an incentive to approximate Epstein’s system, which allows any action that will benefit all participants. When a public goods situation occurs which involves subscribers of several different systems, it would be settled according to prior treaties-when these have been negotiated (for a discussion of similar notions, see [30]). When such treaties have not been negotiated, the public goods problem may go unsolved, and the participants are left with only simple market rules. The penalty for leaving some public goods unprovided may be minor in a computational market ecosystem; no strong example of a public goods problem has so far been proposed.
Even under the selective pressure of competition, it may not be possible to establish a computational legal system that can enforce Epstein’s system well. If so, then the simple, stable, low-overhead rules of the computational market ecosystem will be the system of choice. This system is a simple starting point and enables experimentation with alternatives; experience can show whether any are better.
8. Conclusions
Although evolutionary reasoning is most often applied to biological ecosystems, it is also of use in understanding human markets, culture, and politics, and adaptive computational systems such as EURISKO. By assuming that an ecosystem’s foundational rules will shape its evolutionarily stable strategies, and that these strategies will dominate behavior in the ecosystem, one can relate foundations to emergent properties-including properties sought by a designer. This paper has examined a variety of evolutionary ecosystems and compared them with “direct, idealized-market ecosystems”; for the purpose of evolving useful computational behavior, the latter have strong advantages. Other papers in this volume explore the implementation and properties of computational markets of this sort in greater depth [I,II].
Acknowledgments Listed in “Markets and Computation: Agoric Open Systems”, in this volume.
References
Papers referenced with roman numerals can be found in the present volume: Huberman, Bernardo (ed.), Ecology of Computation (Elsevier Science Publishers/North-Holland, 1988).
[I] Miller, Mark S., and Drexler, K. Eric, “Markets and Computation: Agoric Open Systems”, this volume.
[II] Miller, Mark S., and Drexler, K. Eric, “Incentive Engineering for Computational Resources”, this volume.
[III] Lenat, Douglas B. and Brown, John Seely,, “Why AM and EURISKO Appear to Work”, this volume.
[IV] Kahn, Kenneth, and Miller, Mark S., “Language Design and Open Systems”, this volume.
[V] Rashid, Richard F., “From RIG to Accent to Mach: The Evolution of a Network Operating System”, this volume.
[VI] Perlis, Alan, “The Evolution of Software Systems”, this volume.
[VII] Stefik, Mark, “The Next Knowledge Medium”, this volume.
[1] Dawkins, Richard, “The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design (W.W. Norton and Company, New York, 1986
[2] Hayek, Friedrich A., “Cosmos and Taxis”, in: Law, Legislation and Liberty, Vol. 1: Rules and Order (University of Chicago Press, Chicago, 1973) pp.35-54.
[3] Gardner, Martin, Wheels, Life, and Other Mathematical Amusements (W. H. Freeman, New York, 1983).
[4] Popper, Karl R., “Evolutionary Epistomology”, in Miller, David, (ed.), Popper Selections (Princeton University Press, Princeton NJ, 1985) pp.78-86.
[5] Axelrod, Robert, The Evolution of Cooperation (Basic Books, New York, 1984).
[6] Lenat, Douglas B., “The Role of Heuristics in Learning by Discovery: Three Case Studies“,in Michalski, Ryszard S., Carbonell, Jaime G., and Mitchell, Tom M. (eds.), Machine Learning: An Artificial Intelligence Approach (Tioga Publishing Company, Palo Alto, CA, 1983) pp.243-306.
[7] Dawkins, Richard, The Selfish Gene (Oxford University Press, New York, 1976).
[8] Wilson, Edward O., Sociobiology (Belknap Press/ Harvard University Press, Cambridge, MA, 1975).
[9] Hofstadter, Douglas R., “The Prisoner’s Dilemma Computer Tournaments and the Evolution of Cooperation”, in Metamagical Themas: Questing for the Essence of Mind and Pattern (Basic Books, New York, 1985) pp.715-716.
[10] Smith, Maynard J. and Price, G.R., “The Logic of Animal Conflicts”, in Nature (1973) 246, pp.15-18.
[11] Drexler, K. Eric, “Molecular Engineering: An Approach to the Development of General Capabilities for Molecular Manipulation”, in: Proceedings of the National Academy of Science USA (Sept. 1981) Vol. 78, No 9, pp. 5275-5278.
[12] Drexler, K. Eric, Engines of Creation (Anchor Press/Doubleday, Garden City, New York, 1986).
[13] Rivest, R., Shamir, A., and Adelman, L., “A Method for Obtaining Digital Signatures and Public-Key Cryptosystems” in: Communications of the ACM (Feb. 1978) Vol. 21, No. 2, pp. 120-126.
[14] Miller, Mark S.; Bobrow, Daniel G.; Tribble, Eric Dean; and Levy, Jacob, “Logical Secrets”, in Shapiro, Ehud, (ed.), Concurrent Prolog: Colected Papers (MIT Press, Cambridge, MA, 1987) in press.
[15] Hayek, Friedrich A., Denationalisation of Money (The Institute of Economic Affairs, Westminster, London, 1978, Second Edition).
[16] Keynes, John Maynard, The General Theory of Employment, Interest, and Money (Harcourt Brace Jovanovich, San Diego, CA, 1964).
[17] Wickler, Wolfgang, Mimicry in Plants and Animals (World University Library/ MaGraw-Hill, New York, 1968).
[18] Dawkins, Richard, The Extended Phenotype (Oxford University Press, New York, 1982).
[19] Holland, John H., Holyoak, Keith J., Nisbett, Richard E., and Thagard, Paul R., Induction: Processes of Inference, Learning, and Discovery (MIT Press, Cambridge, MA, 1986).
[20] Ames, Bruce N., Magaw, Renae, and Gold, Lois Swirsky, “Ranking Possible Carcinogenic Hazards”, in Science (17 April 1987) Vol. 236, pp. 271-285.
[21] Nisbett, Richard, and Ross, Lee, Human Inference: Strategies and Shortcomings of Social Judgment (Prentice-Hall, Englewood Cliffs, NJ, 1980).
[22] Haase, Kenneth W., Jr., “Discovery Systems”, in ECAI ‘86: The 7th European Conference on Artificial Intelligence (July 1986) Vol. 1, pp. 546-555.
[23] Hardin, Garret, “The Tragedy of the Commons”, in Science (13 December 1968) Vol. 162, pp. 1243-1248.
[24] Tullock, Gordon, The Organization of Inquiry (Duke University Press, Durham, NC, 1966).
[25] Nelson, Theodor, Literary Machines (published by author, version 87.1, 1987, available from Project Xanadu, 8480 Fredricksburg #8, San Antonio, TX 78229. Available as hypertext on disk from Owl International, 14218 NE 21st St., Bellevue, WA 98007. 1981).
[26] Drexler, K., Eric, Hypertext Publishing and the Evolution of Knowledge (Foresight Institute, Los Altos, CA, 1986).
[27] Kornfield, William A., and Hewitt, Carl, “The Scientific Community Metaphor”, in IEEE Transactions on Systems, Man, and Cybernetics (IEEE, 1981) SMC-11, pp. 24-33.
[28] Kornfield, William A., “Using Parallel Processing for Problem Solving” (MIT AI Lab, Cambridge, MA, 1979) MIT-AI-561.
[29] Hayek, Friedrich A., Unemployment and Monetary Policy: Government as a Generator of the “Business Cycle” (Cato Institute, San Francisco, CA, 1979).
[30] Friedman, David, The Machinery of Freedom: Guide to a Radical Capitalism (Harper and Row, New York, 1973).
[31] Friedman, Milton, and Schwartz, Anna, “The Great Contraction”, in A Monetary History of the United States, 1867-1960 (Princeton University Press/ National Bureau of Economic Research, 1963) Chap. 7.
[32] McGee, John S., “Predatory Price Cutting; The Standard Oil (NJ) Case”, in Journal of Law and Economics (October 1958) 1, 137.
[33] Epstein, Richard A., Takings: Private Property and the Power of Eminent Domain (Harvard University Press, Cambridge, MA, 1985).
[34] Buchanan, James M. and Tullock, Gordon, The Calculus of Consent: Logical Foundations of Constitutional Democracy (University of Michigan Press, Ann Arbor, MI, 1965).
[35] Tullock, Gordon, The Vote Motive (The Institute of Economic Affairs, Westminster, London, 1976).
